|
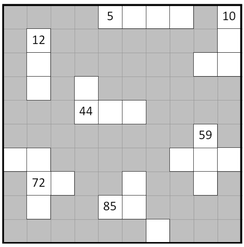
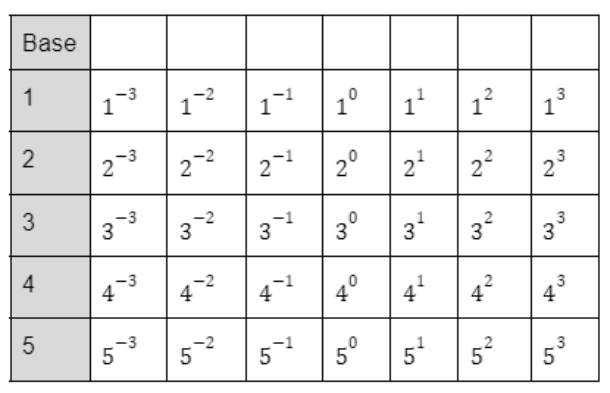
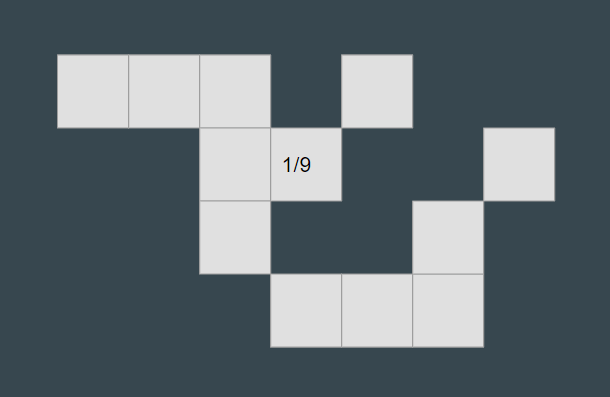
I love my lesson on introducing negative and zero exponents now that I added in the visuals. Check out the lesson here. I also like the lesson I do after where I use smudge math to get them to think about what the exponents should be. BUT, I have come to realize that I need a lesson between the two. My students need more time to work with negative and zero exponents, to play with the patterns, to really get a feel for how the exponents work. I haven't done the lesson with them yet, but following is my plan. Background InformationI am guessing that if you are reading this you are a middle or high school math teacher. Before I share my lesson with you, I want to share a lesson from the primary classroom that inspired me. While scrolling through Twitter, I have come across the fun activities that others have shared of puzzles from the hundreds chart where students have to fill in missing numbers in scattered places of the chart. I love how the activity increases the thinking and adds some play to the learning of the numbers from 1 to 100. My lesson.Depending on where we left off the day before, this lesson may begin with consolidating from the intro lesson. Also, it may need to include talking about what to put in the meaningful notes (this is something I don't normally do, but it will give me a good idea of what they did and didn't learn from the day before).
Ultimately I want the students to become familiar with this chart, with how it moves horizontally and vertically. One extension at this point could be to ask them to continue the rows and columns (if it can be done). Some things I have learned from practicing this lesson on groups of teachers: 1) There is more than one way to fill this in. I was going to fix that by putting another clue in a box, but now I like it because it gives me an extension for the groups that finish quicker than others ("what's another way you could have filled this in?") 2) Students will take a long time reconstructing the grid of the puzzle on the whiteboards. You will save a lot of time if you print this off, put it in a plastic sleeve and tape it to the board Reflection.I really liked how this lesson went with teacher groups I have practiced it with. There were rich discussions amongst math teachers who are experienced with exponents, so I imagine it will be even more beneficial with students learning about the exponents. I also think I will print several different puzzles and use them as quick tasks at the beginning of the class for continued learning and review.
0 Comments
~Objective:
Lesson: I started right away in groups at the boards. We quickly reviewed the structure of slope-intercept form. I then gave the groups a line in standard form and asked them to turn it into slope-intercept form. When they were done, they were supposed use Desmos to check their equation versus the original equation. (I like to use Desmos as an "answer key" whenever I can to connect the algebra with the graph in a natural way). The first equation was 2x+4y = 8 This first one took a while. Many groups had various strategies and I roamed around and visited with them about their ideas. I chose to consolidate right after this problem because there were a few different strategies and I wanted to discuss the pros and cons of each one. There were also some mistakes that we needed to address as a class. (We found that the most efficient strategy was to move 2x and then divide everything by 4). I had the groups then do a 2-3 more problems:
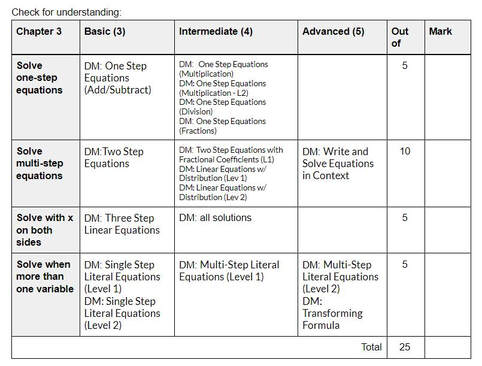
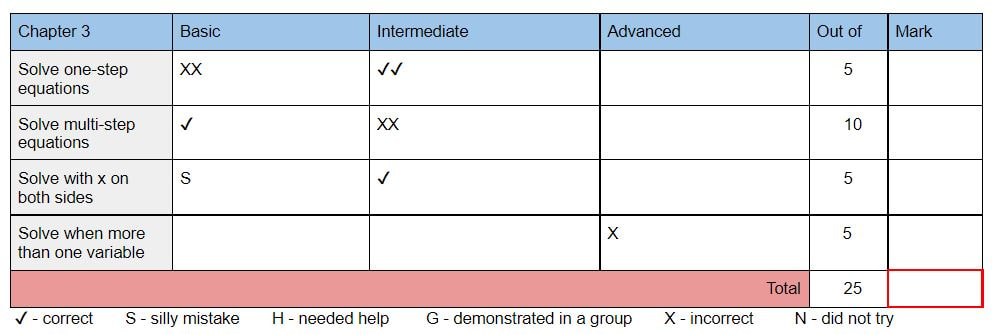
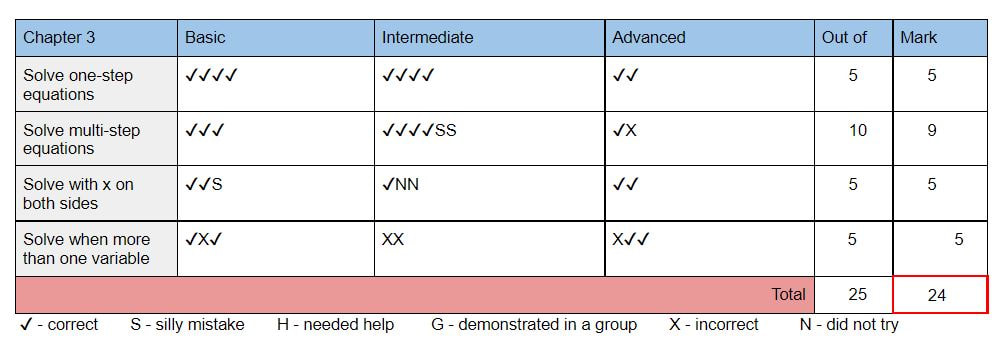
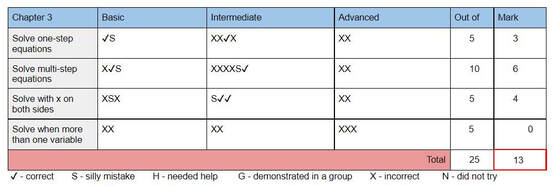
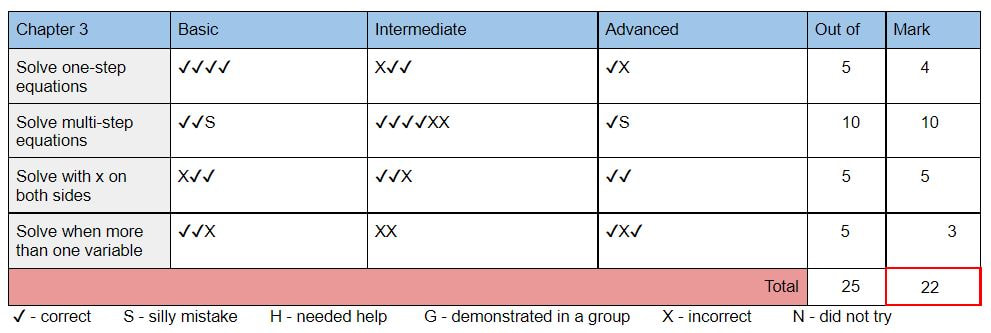
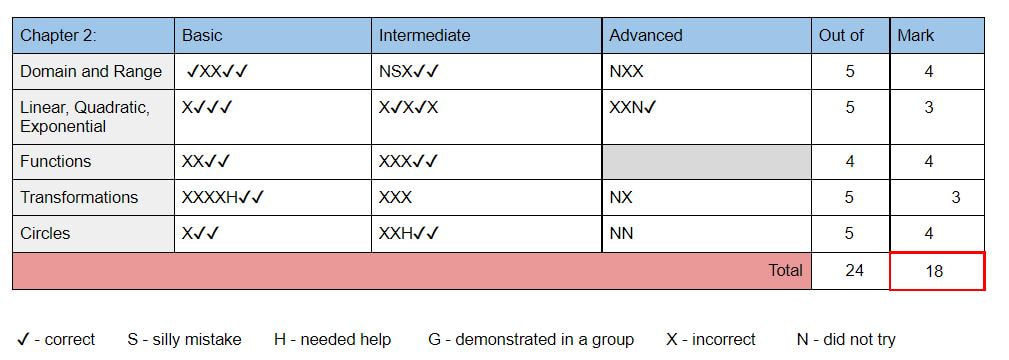
I next wanted to get the students working more individually while I was around to help. I decided to add a little movement and fun with a snowball fight. (I think I got the original idea from Sarah Carter). I put a large set of equations of lines in standard form on the board and gave each student a piece of paper. They chose one equation and wrote it down. Then they crumpled the paper into a ball, I set a timer for 20 seconds, and they threw the snowballs around until the time ran out. Then they each found a snowball and worked out the problem on it so that it was in slope-intercept form. Again, I had them check their work on Desmos. I would have liked to do another snowball fight, but this brought us to the end of the class period. I used Delta Math for Check Your Understanding problems. I have made some big changes this year! I am finally applying all 14 of the Building Thinking Classroom principles and loving it. I did as many as I could before from my research on websites, blogs, podcasts, and interviews. But there were a few principles that I just couldn't grasp until I finally got to read the book. (If you are interested in using BTC, I highly recommend you get the book: BTC). I decided Thanksgiving was a great time to reflect and write about what changes I am making this year and how it is going. I am specifically writing about check understanding, build autonomy, and formative assessment. Most of these are based off the work I did this summer in preparation for the changes. I went through each chapter and decided what I wanted to assess for basic, intermediate and advanced (My grading is 3, 4, 5 since they will be translated into letter grades like the rest of my school). I created a table for each chapter and included it in the meaningful notes packet I make for students at the beginning of the year. You can see an example from Algebra below. 1. Check understanding. I have given homework for a grade my entire career. I have never graded it based on being correct, but instead on completion and showing of work. Doing it this way cut down on how much time I spent on grading since I didn't have to grade each problem for correctness, but I still found myself often wishing the students would go away so that I could get my work done. I needed to grade it all and get it into the gradebook. I hated that part of teaching. I felt like only part of my job was educating students, but the majority of it was correcting and recording work. This year I am no longer grading homework. I still assign problems, but I do not ask them to turn it in. I rarely give problems from the book, but I really like using Delta Math (deltamath.com) for problems. The students get immediate feedback and can see the solution if they get it wrong. I have seen my students put more value into doing their problems correct rather than just getting the problems done with this program. Because I am not correcting/grading their work, the points system doesn't matter, so the students can do as many or as few problems as they would like. Which is another bonus of DM, they can do lots of problems if they would like, where a textbook has a limited number of problems to work on. Reflection: As expected, fewer students are doing the problems than I would like. But, as we do little formative assessments each day, students find out where they are in their own understanding and I see them go back to the DM to practice. They are learning the new system and finding out that they need the practice in some places and not in others. Ultimately, if they are successful in the formative assessments, it doesn't matter to me if they do the DM. (BTW: I just realized have not worried about Photomath once this year!) I created a table for the students to reference which DM assignments align to the topics they will be assessed on (see below). I also include this in the meaningful notes booklet. I have found this table to be useful when helping a student figure out what they can do to get ready for more assessment problems to help improve their grade. 2. Build Autonomy: Managing flow! How do I get my students to help themselves instead of waiting for me to get to them? I was the teacher that would tell my students to steal a problem from another board if they finish and are waiting for me. But then I would leave a group and see two groups just sitting there! Finally, after reading the chapter, I have figured it out. Instead of giving the next problem to the waiting groups, I point at the board that already has the next problem and tell them to take it. (I was enabling them when I would give it to them). Now, my students have started helping themselves instead of waiting for me. Thank Goodness! (This is also true if a group is stuck. I will often tell them to go peek at a certain board to get an idea instead of giving them any help) Another thing I am working on this year is what I do BEFORE groups need help. I used to wait idly and just watch the groups work. Now, I walk to each group, point at a specific item on the board and ask them to tell me about it or to convince me it is right. I am finding the lesson goes much more smoothly than before, I am keeping more involved in their learning, and I am having much richer observations of each and every student. 3. Formative Assessment: I have been trying to figure out standards based grading for years. I have tried a few different things, but none of them felt quite right or worked the way I wanted. I am using the assessment and grading from BTC and I love it! Quizzes. I don't give quizzes any more. I have to admit, when Peter says that you will find you give too many quizzes already, that wasn't true for me. In the first two units this year, I found that we got to the end of the unit and I have very few data collections. I am finding my way though. I try to give one or two problems every day at the beginning of the hour and we call is an "understanding check" instead of a quiz. I also like to use "My favorite no" for these. I make sure the students put their name on them so I can record the data, but it lends itself well to having a purpose in our lesson instead of just a quick check. Quiz reflection: I learned through this process that many students see a quiz as potential punishment. If they aren't ready for the quiz then any problems they do incorrectly lose them points that they can never get back. It is taking me a long time to get them to understand that there are no points taken away for a wrong solution; there will always be more opportunities to show me they can do it. An x at the beginning followed by check marks means they learned, which is the goal. Not all of my students have grasped this yet, but we keep working on it. End of unit test. I hate writing tests. It really is the worst part of my job. Since I am changing how I assess, I have to rewrite all my tests. I am not enjoying it, but it isn't as bad as writing a test from scratch. I use my table (see above) as a guide and make two problems for each cell of the table. I am not completely sure this is what I should do, but it makes sure that a student can possibly get two check marks if they haven't gotten any yet. I do like separating the test into all the basic problems first, followed by all the intermediate problems, and finishing with all the advanced problems like Peter suggests. I find it gives students a reference to where each problem fits in the table. The second worst thing about teaching, after writing a test, is grading a test. However, this has improved with BTC grading. Now I just give it a check mark, x, or S. I don't have to debate how many points to give! Transferring their marks onto their progress tracking sheet is time consuming, but it is easy enough to do that I haven't minded it yet. Test reflection: I was worried the grading would be "inflated" (is that the right word)? At the beginning, students would finish a test and say they failed as they turned it in. But then they would end up with a 20 out of 22. They felt like they failed because they couldn't answer four of the problems in the advanced section. In the past, if they didn't answer four problems, they would have lost a lot of points. But with this, they only lost two points, getting 4 out of 5 on two of the topics. However, when I look over the final grades each time, the letter grade seems very appropriate for each student. So I don't think grades are inflated, they seem to be more appropriate than before. (Side note: this is my 19th year of teaching. Quarter 1 was my very first quarter in my career that I did not have a student fail my class. FIRST TIME EVER! Reflecting on why, I think there were just some students before that found homework to be too big of a workload and could not/would not do it all. I also think that there are so many valuable things we do with all 14 principles that they are just learning better too). Below are a couple examples of the progress tracking sheets for a unit. I put them on a google doc and update it as we go. Students and their parents have access to this sheet at any time. I still have one question about grading. If a student has x's all the way across a row, I will give them a 0 out of 5. But, what if they have a couple check marks sprinkled throughout the row, just not two in a row? Do you give them a 1 or a 2, or do you still give a 0? Improving grades after the test. This has also changed my teaching life. I used to have students stay after school to get help on their homework. Their focus was on getting the assignments done, not necessarily learning the math. I hated it! I do not have the patience for homework help. But now, when a student needs/wants to improve their grade, they stay after with me. We look at their progress tracking sheet and their test to see what they need to learn. The time we spend going over problems is in an attempt to learn, not complete problems. I usually send them on their way with problems to practice. Then we find another time for them to do "assessment" problems to add to their data. Since they only need to do a couple, they can usually get this done during a part of class, at the end of lunch, or during their resource hour. It feels so much more worthwhile now. The students are more focused and aren't coming to me with the stress of a mountain of homework and a checklist to complete. I have also found this useful for a particular student that has extreme test anxiety. We now have scheduled him to come to my room during my prep (his study hall) every Wednesday. We use the time to do some old or new problems and then I can add to his data with my observations instead of just formal assessment problems. It has been a huge help in making sure his grade reflects what he knows. Below is an example of his data after a few Wednesday's of going over a previous chapter. Final Reflection:
After writing all this and rereading it, I realize that there were more things about teaching that I hated than I thought! I really love my job, so I am a bit surprised. But it has also made me realize why I have been leaving the school building earlier than usual and with less weight on my shoulders the last couple weeks. The things that I disliked the most about teaching have changed drastically. I still don't like writing tests, but I don't hate it. Grading them is no big deal. The paperwork of homework and grading is pretty much nonexistent. The time I spend with students is actually teaching rather than assisting with a checklist. I finally feel like the majority of my day is spent educating. I was in love with BTC before because my class changed for my students. They were engaged and THINKING. I have fallen in love with it all over again this year because my class changed for me. I am more engaged, less overworked with tedious tasks, and enjoying how I assess the learning of my students. Objectives:
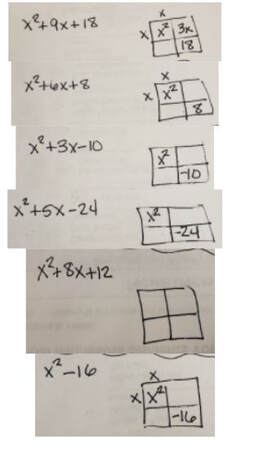
Lesson: I start this lesson at the boards right away. I tell the groups they will be doing the opposite from the lesson before this. I want them to tell me what the two bubbles are that would multiply to give me the quadratic. Their answer should be the two bubbles written out as factors (multiplied). The thin slicing for this is structured that I give them some "clues" but gradually take them away. The series of problems I go through are below. (Please forgive my crude notes, I haven't taken the time to make them more professional). This pretty much takes up most of the class. I consolidate with the class and often give them class time to work on check their understanding problems. I want to make sure they take the time to work on it individually right away.
Objectives:
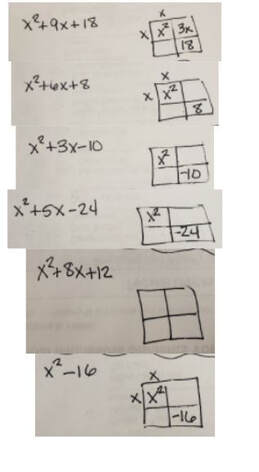
Lesson: I like to start this lesson with a series of notice/wonders or stand and talks. BTC Note: I wonder sometimes if I am giving too much front-loading with the notice/wonders. But they work so well in general that I haven't experimented with the lesson without them. Boards: I get the students into groups and we work through the series of problems pictured below: I like to have an extra challenge ready if a group finished early or before the rest. I often use open middle problems for this reason (and they work really well on VNPS in groups). I love them for everyone, but I especially love them for the students that could use some extra challenging. Below is a good one for this lesson. Finish with a consolidation and meaningful notes. I also give some Delta Math problems for check your understanding practice.
Note: this is a simply designed lesson focused on the Thinking Classroom (TC) structure. I left out the commentary that would explain the teacher moves that go with the TC and how to run a "What do you Notice". The goal for students is specific, factor by grouping. Objectives:
~Preknowledge:
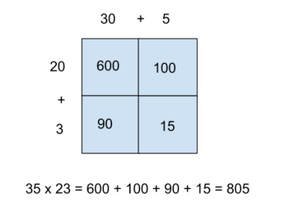
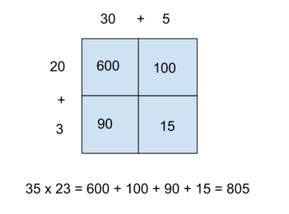
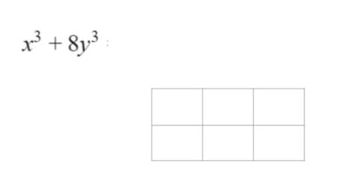
Lesson: Have the students multiply the two problems pictured below (using the area model). Then have the class do a Notice/Wonder with the results. (the problems were designed to be very similar with minimal changes to help focus on the difference in the factors that create a 4-term polynomial instead of a trinomial). Send the students to the whiteboards in random groups to factor the progression of problems that can be factored with grouping (using an area model) Make sure to finish with a 4-term polynomial that cannot be factored by grouping. Have students take notes on what they learned. Here are the google slides I used to teach during distance learning. The slides contain the problems ready to be copy/pasted into a jamboard.
Note: this is a simply designed lesson focused on the Thinking Classroom (TC) structure. I left out the commentary that would explain the teacher moves that go with the TC and how to run a "What do you Notice". The goal for students is specific, factor sum and difference of cubes. Objectives:
~Preknowledge:
Lesson: What do you notice: factorizations of difference of squares (focus on the factors contain the square root of the original terms) What do you notice: factorizations of sum and difference of cubes (focus on the first factor and how it is the cube roots of the original terms, the contents of the 2nd factor are not important until they figure it out during the TC portion) Move students to the whiteboards in random groups. Give one problem at a time where students figure out the factoring. The last problem needs to have a monomial factored out first. Finish with students taking notes on what they learned.
Final Thoughts: I am not sure if giving the students a 2 by 3 box to start with is too much scaffolding. I will play around with this in the future. Here are the google slides I used for distance learning. The images are ready to be copy/pasted in the jamboard. The Prelude.I attended an Ethnomathemtics workshop about two years ago. I have always been fascinated by cultures, my own and others. The chance to tie mathematics into such an interesting topic was an opportunity I couldn't resist. One the presenters was Dr. Jim Barta from Bemidji State University. There were two things that he brought to the workshop that inspired me: the cultural interview and story cards. I saw both of these activities as tangible things that math teachers can do in our classrooms to get students to see mathematics in their cultures and to use their cultures in our mathematics classroom. (There is a lot more to this back story, but that will have to wait for another post). I have since experimented with both of these things, but now I want to get serious. I am doing my research and planning my lessons. I want to build a unit that other teachers can use in their classrooms. I want to build something that helps us build a sense of belonging for our students in our classrooms. I figure I have two types of students to consider here: 1) The students whose cultures are still beautifully immersed in their heritage. They can see many of their family's traditions as passed down from previous generations. I think of my good friend May who is Hmong and can tell me about so many customs that have been passed down through the generations. 2) The students who are a product of the melting pot that is the United States. Their family's traditions change with each generation as parents from different cultures create new traditions, or combine traditions, to work for their new family. I think of myself. My mother is German and my father is a combination of various Scandinavian ancestries. Neither share stories about why we do certain traditions during the holidays and other times. The closest comes to our Christian beliefs and traditions, but the actual tie to family culture and historical connection feels lost. (Of course, there will be students at various places between these two) Through this unit, we are going to focus at two levels:
The Outline of the Unit (so far).
My Final Thoughts
Today I was listening to the Making Math Moments Podcast, episode 98 with Peter Liljedahl and decided I wanted to write my reflection of what I learned from it. I fell in love with the Thinking Classroom over two years ago. Since then I have been studying articles, reading books, listening to podcasts, and exploring; basically doing anything I can to learn more and teach better. When Covid-19 changed our classrooms to online environments, I refused to go back to lecturing. I used Jamboards and Zoom breakout rooms to keep my kids going. It worked pretty great and so I planned to keep doing that during the new school year. I started the year with 4 classes of students who were in my class last year, they were already familiar with working on whiteboards and learning through the Thinking Classroom. I also had 2 classes of student who were in my classroom for the first time and haven't been introduced to the Thinking Classroom yet. Also this year, I am teaching Hybrid. Half my students are in my physical classroom, half are at home attending through a live zoom link. I am super grateful for the technology that my school has made available for this as I feel that I can pretty seamlessly teach both groups at the same time. During the 8 weeks of school we have had so far, I have been putting my in-person students on the whiteboards and my at-home students on Jamboards while working together in breakout rooms. It has not been going as well as it did in the spring. Over the last 4 weeks, I have been trying to figure out what to change while still honoring the 14 guidelines of the Thinking Classroom. Thanks to the podcast episode, I think I am ready to make some (informed) changes for Monday! My frustrations and possible solutions: My College Algebra class has not been doing well. They complain that when they are at home, the breakout rooms do not go well. They tell me that they are only learning during the consolidation time and the breakout room time is a waste. I actually quit doing the breakout rooms for two weeks, which broke my heart. But their tests have been backing up their claims of not learning. This week, I had a heart-to-heart with the class about what needs to change to help them learn and they all chimed in that they want to be back at the boards. So my new mission is to get them back to the boards. So here are the issues I have been battling during Hybrid learning and what I am going to try differently. 1) Most of my seniors and juniors no longer have a touchscreen device. The amount work they have to do to write on the Jamboard has become enough of a nuisance that their boards are blank at the end of the hour. Besides that, the work space on a Jamboard is way too small. In my visit with my seniors, they all felt that having a physical whiteboard at home would help with groupwork in breakout rooms. So I called up the local lumberyard, ordered three sheets of shower board, had the shop class cut them into 2 foot by 2 foot pieces and handed them out to each student in College Algebra to keep at home. If this works, I will get more to hand out to the rest of my classes. 2) Random groupings of 3. In person, a random group of 3 is best, I have seen this over and over. But I have been questioning the "3 in a group" part this fall. I have heard from many students that being in a "bad group" means that they do all the work on their own and there is no interaction. I suppose this happens for many reasons, one of them being that I cannot easily monitor the groups and intervene when needed. (I wish there was a way to be able to see each breakout room simultaneously to make sure they are unmuted and interacting. I can monitor the Jamboard, but watching them write does not guarantee interaction and discourse). I have been playing around with the idea of having more students in a group. I was excited to hear that Peter Liljedahl also found the same problem and that 4 or 5 students in a virtual group worked better. (Listen to the podcast to hear the research behind the number in a group). So I plan to now randomly assign my students into groups of 4 or 5 during virtual breakout groups, still 3 when in person. 3) I don't like that I cannot listen in to the zoom breakout groups easily. During distance learning in the spring, I would hop between breakout rooms and check on each group. This worked relatively well. However, now that I am physically in a room of students who are physically distanced while working together and talking with masks on, my joining a group is almost impossible. They can't hear me, I can't hear them. I don't have a solution. But I did like Peter's suggestion of having a discussion board where virtual groups can list what they found difficult and how they worked through those difficulties. I am thinking I might assign some of that. Maybe have someone in the group keep a "group diary" summarizing their time?
4) I am horrible at leaving time for meaningful notes. This is even true for my non-Covid 19 teaching. The podcast was the first time I heard them referred to as "notes for your future, forgetful self". I love that. I am going to start assigning that for post class time each day. I have spent this first quarter modeling how to fill it in, I think my students are ready for it to be independently assigned for post-class reflection. 5) I still need to work on the "homework" part. But I am feeling overwhelmed and overworked, so I am going to be okay with that being left for future improvements. Although that is really hard for me. And that is what I learned today. I am looking forward to creating my lesson plans for the week. I hope to get back to feeling like I am living the dream of every teacher: engaged students, deep thinking, and great discussions. And I am confident that if I don't get to the great REM cycle dream, I can at least reach the daydream level. I keep seeing Sara Vanderwerf tell people on Twitter that I have some great thinking on this. So I decided I need to blog about my ideas so that I have something I can share with people. (I do not claim to be the best or know the best for all of this, I am just sharing my ideas). First off, my decisions on how I am teaching, whether in the classroom or from a distance are always founded in the Thinking Classroom. This is a set of elements that were researched and organized by Peter Liljedahl. Since I have built my classroom into a Thinking Classroom, my class has become a student-centered, engaged room that gets kids thinking and motivated to figure things out for themselves while also helping each other. If you are not familiar with the Thinking Classroom, I am sharing my google slides and recording of a presentation I did with MDE and MCTM this summer. MDE is working on making the presentation accessible, but in the meantime, the raw recording is below. Link --> Google Slides: The Thinking Classroom Distance Learning Last Spring My school is 1-to-1 chromebooks and we were able to get internet to every home. Most of what I did was Synchronous. Although what I did can be done using other platforms and technology, here is my list:
Here is a video of what I did in the Spring and what I plan to do during Virtual days (every Wednesday for my school, we are hybrid the other days) Link --> Google Slides Hybrid Learning My school is starting with hybrid learning in the high school. I am intrigued to try it, but have a few worries about the execution. We will see. My goal is to still have a Thinking Classroom. I will be blending much of what I do in the classroom and what I did during distance learning. I will be using:
My school put together a little video showing what our hybrid model will look like. It also shows how the OWL works. You can see it here. Here is a video that explains more of my plans for hybrid. Asynchronous Learning Although this is not something that I have to do, I have some ideas. Thanks to my friend, May Vang Swanson, they are even better than what I was thinking on my own. My goal, as always, is to do as much as I can with the Thinking Classroom. Here is my list of what I would use:
As you can see above, one thing that I would add to what I use is Flipgrid. From what I have heard from May and others, it would very much help with making this student-friendly and as mush student discourse as you can get asynchronously. Here is a video explaining what I would imagine Asynchronous would look like. Link ---> Google Slides I hope this is able to help spark some ideas for your classroom. I do not claim to be a know-it-all for technology. So, if you have a great app, website, or resource that would help someone that cannot use what I have used, please share it in the comments.
Manipulatives I am a huge advocate of using manipulative at all levels of mathematics. During a pandemic, we have some challenges:
Good luck to everyone this year. If you would like to visit or as a question, feel free to add a comment, email me ([email protected]) or find me on twitter (@strom_win). |
AuthorI teach mathematics for grades 7-12. Teaching mathematics is my passion. Archives
August 2022
Categories
All
|


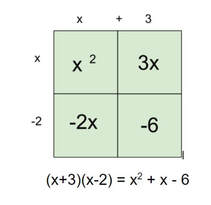
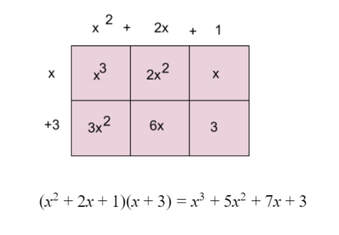
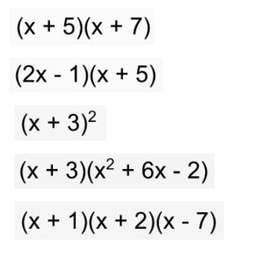
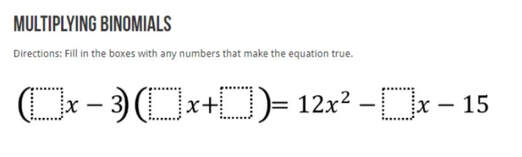
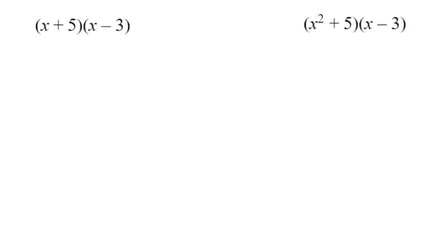
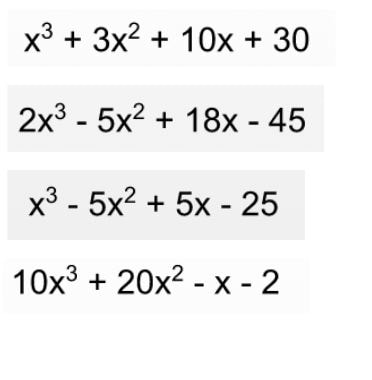
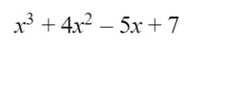

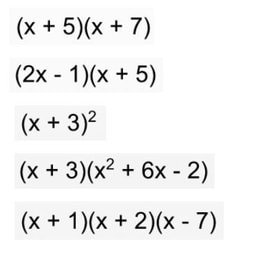
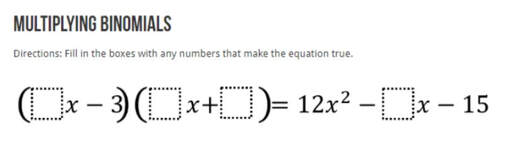


 RSS Feed
RSS Feed
